Vlad Vicol and I have just uploaded our paper “Anomalous diffusion by fractal homogenization” to the arxiv. It contains results previously announced last June at the “Probability and Mathematical Physics” conference in Helsinki and in subsequent seminar talks by both of us since then. (A recording of my Helsinki talk can be found here.)
In this post I’m going to give an informal summary of the results in the paper and the motivation behind them.
What is “anomalous diffusion”?
Consider the initial-value problem for an advection-diffusion equation
(1) 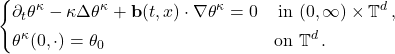
The vector field ![]() is assumed to be a divergence-free vector field,
is assumed to be a divergence-free vector field,
(2) ![]()
and we think of it as the velocity of an (incompressible) fluid. The solution ![]() of this equation is “the scalar.” It is quantity, like temperature or the concentration of a dye, which diffuses in the fluid and is also advected by the fluid flow. The given parameter
of this equation is “the scalar.” It is quantity, like temperature or the concentration of a dye, which diffuses in the fluid and is also advected by the fluid flow. The given parameter ![]() governs the rate of diffusion of the scalar in the fluid on infinitesimal scales. In the fluids context, this equation is sometimes called the “passive scalar equation” because the scalar is “passive” in that it is advected by the fluid flow, but does not affect the flow.
governs the rate of diffusion of the scalar in the fluid on infinitesimal scales. In the fluids context, this equation is sometimes called the “passive scalar equation” because the scalar is “passive” in that it is advected by the fluid flow, but does not affect the flow.
We are interested in the case that ![]() is very small. If the vector field is nice enough—for instance, if it is Lipschitz continuous in the space variable
is very small. If the vector field is nice enough—for instance, if it is Lipschitz continuous in the space variable ![]() —then solutions of the equation (1) will converge as
—then solutions of the equation (1) will converge as ![]() to the unique solution of the first-order transport equation
to the unique solution of the first-order transport equation
(3) ![]()
The solution of (3) is unique because the ODE trajectories ![]() are well-defined by the assumed Lipschitz continuity of
are well-defined by the assumed Lipschitz continuity of ![]() and the Picard-Lindelöf theorem.
and the Picard-Lindelöf theorem.
The ![]() norm of the scalar
norm of the scalar ![]() is monotone decreasing in
is monotone decreasing in ![]() , and in fact its time derivative can be computed explicitly, using the equation (1) and the incompressibility condition (2). We have:
, and in fact its time derivative can be computed explicitly, using the equation (1) and the incompressibility condition (2). We have:
(4) ![]()
The transport equation meanwhile preserves all ![]() norms of its solution in time, because the flows of the vector field are measure-preserving. Therefore the convergence
norms of its solution in time, because the flows of the vector field are measure-preserving. Therefore the convergence ![]() in
in ![]() implies that the dissipation of scalar variance vanishes in the limit
implies that the dissipation of scalar variance vanishes in the limit ![]() :
:
(5) ![]()
If the vector field ![]() is rougher than Lipschitz in space, the dissipation of scalar variance may fail to vanish in the limit of small
is rougher than Lipschitz in space, the dissipation of scalar variance may fail to vanish in the limit of small ![]() . We say that the advection-diffusion equation exhibits anomalous dissipation of scalar variance if
. We say that the advection-diffusion equation exhibits anomalous dissipation of scalar variance if
(6) ![]()
This is also called anomalous diffusion.
Why is anomalous diffusion interesting?
According to physicists, anomalous diffusion is a signature of (passive scalar) turbulence, and should be expected of vector fields ![]() which have certain properties of a turbulent fluid. The story they tell is about the flow of energy across length scales, from large scales to small scales. If
which have certain properties of a turbulent fluid. The story they tell is about the flow of energy across length scales, from large scales to small scales. If ![]() is very small, then the vector field is dominant on all length scales above a very small scale (called the inertial scale).
is very small, then the vector field is dominant on all length scales above a very small scale (called the inertial scale).
What is supposed to happen is that the wiggles in the vector field interact with wiggles in the scalar, which creates wiggles in the scalar on a scale one order of magnitude smaller. These wiggles then interact again with the wiggles in the vector field on that scale, and the process repeats over and over. This process does not reduce the ![]() norm of the scalar, because the vector field is divergence-free. But, eventually, the scalar develops wiggles on the inertial scale, where the diffusion term
norm of the scalar, because the vector field is divergence-free. But, eventually, the scalar develops wiggles on the inertial scale, where the diffusion term ![]() can destroy them. This results in a loss of
can destroy them. This results in a loss of ![]() norm, and the incredible prediction is that it should happen by time
norm, and the incredible prediction is that it should happen by time ![]() no matter how small
no matter how small ![]() is!
is!
The picture of energy moving into small scales due to advection (called an energy cascade) before finally being destroyed by viscosity is core to phenomenological theories of turbulence. It is also a very old idea, famously summarized in 1922 in a poem by Richardson:
Big whirls have little whirls
that feed on their velocity,
And little whirls have lesser whirls
and so on to viscosity.
The version of this idea discussed above is the passive scalar version of this concept, which is perhaps simpler to analyze since the solution ![]() is decoupled from the vector field
is decoupled from the vector field ![]() .
.
It turns out to be very difficult to formalize this physical intuition, due to the large number of interacting scales. In fact, the mathematical theory is so far behind the physics that we have very few examples of vector fields which exhibit anomalous diffusion, and the examples we do have are quite limited.
The main result of the paper
The goal of our work is to develop new analytic tools for proving anomalous diffusion. In this first paper, we build an explicit vector field which exhibits anomalous diffusion for every (![]() ) initial datum
) initial datum ![]() . The vector field is not the solution of a fluid equation, but has “fluid-like” properties and competes with other models of “synthetic turbulence”. The picture of the cascade is apparent in our proof, which is a renormalization-group like argument in which we coarse-grain the equation, scale-by-scale, starting from the smallest scales. As we go up the scales, the renormalized diffusivities increase until they are of order one on the largest macroscopic scale (also of order one). This implies the diffusive anomaly.
. The vector field is not the solution of a fluid equation, but has “fluid-like” properties and competes with other models of “synthetic turbulence”. The picture of the cascade is apparent in our proof, which is a renormalization-group like argument in which we coarse-grain the equation, scale-by-scale, starting from the smallest scales. As we go up the scales, the renormalized diffusivities increase until they are of order one on the largest macroscopic scale (also of order one). This implies the diffusive anomaly.
This renormalization perspective is very old—in fact, the idea goes back to the 19th century! (See Section 9.6 of Frisch’s book for a very informative discussion of this.) But, it has never been made into a mathematical proof before, presumably due to the technical difficulty in doing so. We managed to accomplish this using techniques from quantitative homogenization, which is how we pass from one scale to the next. The arguments in our paper are indeed quite long and technically demanding, but we hope they serve as a “proof of concept” that it is possible to formalize a cascade due to advection, and that homogenization/renormalization methods are good analytic tools for doing so.
Here is a more precise version of our main result.
Theorem (A.-Vicol 2023) Let ![]() and
and ![]() . There exists a vector field
. There exists a vector field ![]() which belongs to
which belongs to ![]() and a subsequence
and a subsequence ![]() with
with ![]() such that, for every mean-zero initial datum
such that, for every mean-zero initial datum ![]() , the (unique, classical) solutions of the initial-value problem (1) with
, the (unique, classical) solutions of the initial-value problem (1) with ![]() satisfy
satisfy
(7) ![]()
where ![]() depends only on the ratio
depends only on the ratio ![]() .
.
How this fits into the existing literature
There are two kinds of previous results of which we are aware.
The first is the Kraichnan model, introduced by Kraichnan in 1968, in which the vector field ![]() is taken to be a Gaussian random field which is white-in-time (no correlations) and colored-in-space (correlations decay like a certain power of the distance). This model allows for certain exact computations on the statistics of the scalar, and due to this it has been extensively studied, and anomalous diffusion was proved by Bernard, Gawedzki, and Kupiainen (1998). The downside is that while the white-in-time behavior is needed for the exact computations, this is not a very physical assumption. In fact, it is probably responsible for the whole diffusion anomaly. Indeed, a vector field which is very rough in time almost acts like a forcing term, so that the equation roughly looks like
is taken to be a Gaussian random field which is white-in-time (no correlations) and colored-in-space (correlations decay like a certain power of the distance). This model allows for certain exact computations on the statistics of the scalar, and due to this it has been extensively studied, and anomalous diffusion was proved by Bernard, Gawedzki, and Kupiainen (1998). The downside is that while the white-in-time behavior is needed for the exact computations, this is not a very physical assumption. In fact, it is probably responsible for the whole diffusion anomaly. Indeed, a vector field which is very rough in time almost acts like a forcing term, so that the equation roughly looks like ![]() , and so it is not hard to see why this should create diffusive behavior (which is perhaps not as anomalous after all).
, and so it is not hard to see why this should create diffusive behavior (which is perhaps not as anomalous after all).
The second set of results are much more recent. It began with the work of Drivas, Elgindi, Iyer and Jeong (2019), who gave the first example of an initial datum and a vector field—which is at least continuous in space and a function in time (as opposed to a distribution)—and admits anomalous diffusion. Their example is deterministic. The idea is to have shear flows which alternative between horizontal and vertical, and focus and intensify up to a “blow-up time” ![]() , when all the anomalous diffusion happens. Notably, their construction works for any
, when all the anomalous diffusion happens. Notably, their construction works for any ![]() , which means that the vector field may be almost Lipschitz, a sharp result.
, which means that the vector field may be almost Lipschitz, a sharp result.
This example was modified and extended in recent papers by Colombo, Crippa, and Sorella (2022) and Brue and De Lellis (2022). These papers used a similar construction and furthered the analysis of [DEIJ] in several ways. The first work [CCS] proves a ![]() estimate (
estimate (![]() is tiny) for the scalar
is tiny) for the scalar ![]() which is uniform along the subsequence
which is uniform along the subsequence ![]() which has the anomaly. This is not a regularity estimate per se, since the scalar is constructed with the vector field, but it is valid for the whole range
which has the anomaly. This is not a regularity estimate per se, since the scalar is constructed with the vector field, but it is valid for the whole range ![]() . In [BDL], the passive scalar equation is essentially embedded into a Navier-Stokes equation with forcing by adding an extra dimension (with the forcing being what you get when you plug the vector field into the Navier-Stokes operator), leading to results in the direction of “anomalous dissipation for forced Navier-Stokes.”
. In [BDL], the passive scalar equation is essentially embedded into a Navier-Stokes equation with forcing by adding an extra dimension (with the forcing being what you get when you plug the vector field into the Navier-Stokes operator), leading to results in the direction of “anomalous dissipation for forced Navier-Stokes.”
In each of these works, the spatial cascade is not present in the sense that only one scale is active in both the vector field and the scalar, at each time. Moreover, the anomalous diffusion is not known to hold for all initial data, or even all sufficiently smooth data, since the scalar is constructed at the same time as the vector field.
(A more complete and systematic review of the literature is presented in Section 1.1 of our paper.)
Construction of the vector field and proof of the theorem
We give an extensive overview of the main ideas in the proof of the above theorem in the introduction of our paper (see Section 1.2). But let’s quickly review the ideas here.
The vector field ![]() constructed in the above theorem is explicit and has a fractal-like structure. We give the construction only in dimension
constructed in the above theorem is explicit and has a fractal-like structure. We give the construction only in dimension ![]() because two-dimensional notation is simpler and more convenient (the result in higher dimensions is not more difficult). We take constant-in-time shear flows and alternate the direction of the flow (between horizontal and vertical) in time as our “base fractal” and we insert these into the the vector field along a sequence of scales
because two-dimensional notation is simpler and more convenient (the result in higher dimensions is not more difficult). We take constant-in-time shear flows and alternate the direction of the flow (between horizontal and vertical) in time as our “base fractal” and we insert these into the the vector field along a sequence of scales ![]() , one at a time. This gives a sequence
, one at a time. This gives a sequence ![]() of smooth vector fields, and we eventually define
of smooth vector fields, and we eventually define ![]() .
.
These are defined recursively (roughly) as follows. Having defined ![]() , we define
, we define ![]() by adding to
by adding to ![]() a copy of the alternating shear flow, dilated so that it lives on scale
a copy of the alternating shear flow, dilated so that it lives on scale ![]() , after composing it with the inverse of the flow of the vector field
, after composing it with the inverse of the flow of the vector field ![]() . We choose the size of the shear flows to be
. We choose the size of the shear flows to be ![]() , which is consistent with
, which is consistent with ![]() belonging to
belonging to ![]() . The vector field
. The vector field ![]() has shear flows active on each of length scales
has shear flows active on each of length scales ![]() , but no smaller scales, and it is essentially the vector field
, but no smaller scales, and it is essentially the vector field ![]() with all wiggles below
with all wiggles below ![]() erased.
erased.
To prove that the vector field ![]() we have constructed exhibits anomalous diffusion for the corresponding passive scalar equation, we construct an increasing sequence
we have constructed exhibits anomalous diffusion for the corresponding passive scalar equation, we construct an increasing sequence ![]() of “renormalized diffusivities” such that the equation
of “renormalized diffusivities” such that the equation
(8) ![]()
homogenizes to the equation
(9) ![]()
In other words, the equation for ![]() is effectively the same as the one for
is effectively the same as the one for ![]() : the effect of the wiggles at scale
: the effect of the wiggles at scale ![]() in the vector field
in the vector field ![]() is to increase the (effective or renormalized) diffusivity from
is to increase the (effective or renormalized) diffusivity from ![]() to
to ![]() . This is due to the enhancement of diffusivity due to advection, which is a well-studied topic in homogenization theory. The sequence
. This is due to the enhancement of diffusivity due to advection, which is a well-studied topic in homogenization theory. The sequence ![]() satisfies a recurrence relation which is based on the enhancement due to a single shear flow (with one active scale). Each number
satisfies a recurrence relation which is based on the enhancement due to a single shear flow (with one active scale). Each number ![]() represents the diffusivity acting on scale
represents the diffusivity acting on scale ![]() , and is analogous to what is called “eddy diffusivity” in fluids. In this way, our argument can be considered a renormalization group-type argument.
, and is analogous to what is called “eddy diffusivity” in fluids. In this way, our argument can be considered a renormalization group-type argument.
Until now, homogenization theory has mainly been used to study situation in which there are two scales which are asymptotically well-separated. What makes our work different is that we have infinitely many active scales, which are not well-separated, and must be homogenized one-by-one in a “homogenization cascade.” This requires a quantitative argument which, even though the shear flows are perturbations of periodic functions, is quite involved.
Ongoing work
There are more results that we have announced in our talks than are contained in this paper, and there is a second paper on the way which we are writing jointly with Keefer Rowan. In this forthcoming paper, we will prove certain uniform regularity estimates on the scalar ![]() which have importance implications for the understanding of the behavior of the scalar on all length scales. In particular, we prove that, for any
which have importance implications for the understanding of the behavior of the scalar on all length scales. In particular, we prove that, for any ![]() , the vector field can be constructed in such a way that the scalar
, the vector field can be constructed in such a way that the scalar ![]() belongs to
belongs to ![]() uniformly along the subsequence
uniformly along the subsequence ![]() which witnesses the diffusion anomaly. This is sharp in the sense that regularity better than
which witnesses the diffusion anomaly. This is sharp in the sense that regularity better than ![]() would imply no diffusive anomaly by the commutator estimate of Constantin, E, and Titi (1994). It can be thought of as a uniform (
would imply no diffusive anomaly by the commutator estimate of Constantin, E, and Titi (1994). It can be thought of as a uniform (![]() type) upper bound to match the lower bound given by (7).
type) upper bound to match the lower bound given by (7).
This uniform Hölder estimate allows us to understand that fine structure of the parabolic Green function for the advection-diffusion operator on smaller time and length scales, which has other important consequences. For instance, we learn that the condition on the initial condition ![]() can be relaxed from
can be relaxed from ![]() to
to ![]() and that the number
and that the number ![]() in (7) is actually universal, and does not depend on
in (7) is actually universal, and does not depend on ![]() .
.