Tuomo Kuusi and I have written a new book-length manuscript with the title “Elliptic Homogenization from Qualitative to Quantitative” which we have just posted to the arxiv. This is intended as an introductory text for graduate students and researchers interested in quantitative homogenization for elliptic equations in divergence form. We assume no previous knowledge of the topic and begin with a detailed presentation of the qualitative homogenization theory. By the end of the text, the reader should have a fairly complete view of the main ideas and results in quantitative homogenization and be able to read the latest research articles.
Homogenization, for those who don’t know, is the term used for an asymptotic limit of a certain kind of singular perturbation problem in PDEs. This description makes it seem very boring and obscure, so let me try again. Homogenization is a topic at the interface of mathematical analysis, PDEs, probability and statistical physics which is about inventing analytic tools, often using PDE methods, for studying disordered systems exhibiting behavior on several very different length scales.
The model problem which has received a lot of attention in the last decade is the elliptic equation ![]() in which the diffusion matrix
in which the diffusion matrix ![]() is a stationary random field, and we wish to understand the behavior of solutions on large scales. This particular model and variants of it are hiding in a surprising number of probability and statistical mechanics problems. So it is important to understand it well, and the project of quantitative homogenization is, as the name suggests, to go beyond soft limits and get rates of convergence, understand the next order correction terms, and so forth. Active work on this topic began around 2009 with the work of Gloria & Otto, and since then the theory has been developed by main two main teams: Gloria & Otto and their collaborators (the “Leipzig group”) and a second group consisting of Kuusi, Jean-Christophe Mourrat, Charles Smart, myself and our collaborators.
is a stationary random field, and we wish to understand the behavior of solutions on large scales. This particular model and variants of it are hiding in a surprising number of probability and statistical mechanics problems. So it is important to understand it well, and the project of quantitative homogenization is, as the name suggests, to go beyond soft limits and get rates of convergence, understand the next order correction terms, and so forth. Active work on this topic began around 2009 with the work of Gloria & Otto, and since then the theory has been developed by main two main teams: Gloria & Otto and their collaborators (the “Leipzig group”) and a second group consisting of Kuusi, Jean-Christophe Mourrat, Charles Smart, myself and our collaborators.
Since we have already written a book on the same topic (jointly with Mourrat) about five years ago, I’d like to explain in this post the reason we decided to write a second manuscript so soon after finishing that one, and how it differs from the first one.
Executive Summary
1. This is much more of an introductory text, and more gentle to non-experts. The text is self-contained, and we think it is suitable for a graduate topics course. The first part of the book covers the qualitative theory of homogenization in detail, even providing proofs of the basic ergodic theorems, so it should be readable for those with no prior knowledge of homogenization theory. The second chapter is about the probabilistic interpretation of homogenization in terms of CLTs for Markov processes, which we hope will make things easier on readers with a background primarily in probability (as opposed to PDE). We have also emphasized the coarse-graining and renormalization group perspective on the theory, which we hope will have some appeal to a mathematical physics audience. The end goal is to explain the optimal quantitative estimates on the first-order correctors, so we do not go deeper into the theory than that (at least in this initial draft).
2. The parts that overlap our previous book are much better. The quantitative homogenization theory is very technical and it takes a lot of work to compress the proofs into a format people outside the field can appreciate and digest. We tried to do this in writing our last book, but we realized later that there were still a lot of improvements to be made. This has taken years, but in this new manuscript we think we have presented the core of the theory as simply as possible. In particular, while Chapters 4-8 overlap a lot with Chapters 2-4 & 10 of the previous book, the presentation here is far superior. We would definitely recommend that non-experts trying to learn the topic make this new manuscript their starting point! (An exception is Chapter 3 of the previous book, on the large-scale regularity theory, which we felt we couldn’t really improve upon very much.)
3. The theorem statements have been generalized. Notably, we introduce a new quantitative ergodicity (“mixing”) assumption. Some people are very interested in homogenization results under weaker mixing conditions, and in which methods can be used to prove the best results under various hypotheses on the coefficients. In fact, one of the annoying things in the stochastic homogenization community is that different groups were using different sorts of assumptions, and this makes it more difficult to cite and to compare different results. For instance, in the past, we have mostly used a finite range of dependence assumption, while the Leipzig group has favored spectral gap or log Sobolev inequality type assumptions. Our new mixing condition covers each of these cases at once, and basically all the ones used previously in the literature. We are able to prove, under such general assumptions, optimal estimates—making it clear the renormalization strategy produces optimal estimates in all of the main examples. We hope this helps to clarify the situation and unifies different results proved previously, as well as make our presentation a useful reference going forward.
4. There are some new results. We prove the sharp Gaussian-type moment bounds at the critical scaling for the fluctuations of the correctors, in the case that the diffusion matrix ![]() is a local function of a stationary, Gaussian random field (exhibiting power-like decay of correlations). This has been conjectured since at least 2015 by the Leipzig group, but has remained without proof until now. It seems to us that an approach based on renormalization is needed to prove such a result, and one based on the spectral gap or LSI will necessarily lead to sub-optimal stochastic moments. (For insiders: we also have a slightly sharper stochastic moment estimate for the minimal scale in the large-scale regularity theory, now on top of the exponent for all orders of regularity, under general assumptions.)
is a local function of a stationary, Gaussian random field (exhibiting power-like decay of correlations). This has been conjectured since at least 2015 by the Leipzig group, but has remained without proof until now. It seems to us that an approach based on renormalization is needed to prove such a result, and one based on the spectral gap or LSI will necessarily lead to sub-optimal stochastic moments. (For insiders: we also have a slightly sharper stochastic moment estimate for the minimal scale in the large-scale regularity theory, now on top of the exponent for all orders of regularity, under general assumptions.)
This manuscript began as a set of notes to accompany a course I gave at the summer school “Journées équations aux dérivées partielles” which took place in Obernai, France, in June 2019. The students taking my graduate topics course at Courant in the fall of 2019 were told to expect a full set of course notes “within a couple of weeks,” which some of them still crack jokes about. There is an editor & colleague who has been patiently waiting for two years for us to complete it. Obviously it took Tuomo and I more time to finish and polish these lecture notes than we forecast, and we’d like to thank everyone for their patience.
We welcome any comments, either here or privately by email. (If you find typos, please tell us!)
Our plan going forward is to treat this almost like a software project, with periodic versions improving and expanding the text. We already have specific ideas for more chapters to write. Since we don’t want to have to write a third book once we begin to realize the shortcomings of this one, we intend to keep the copyright so we can continue to iterate and improve it. We will use this GitHub repository for version control and transparency, with more infrequent updates to the arxiv posting.
Thanks for your notes which is very helpful for me to learn this topic.
I have a confusion about the statement of Thm 1.21. Should we assume r > 2 \Chi but not r > \Chi? If so, in (1.172), s is larger than \Chi and the error of correctors is smaller than \delta.
Additionally, it seems that L^2 norm of u-u_bar can be controlled by H-1 norm of the gradient, but I didn’t find a proof. (I know the proof for H-1^hat norm, but in chapter 1 we only use H-1 norm.) Could you give me a reference for the proof? Thanks. I guess my question might be stupid, because I am not familiar with PDE before.
(Sorry for the late reply to your comment, which I missed until now.)
1. Yes, probably there is a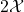 that should be there instead of
that should be there instead of 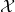 , but not in the statement of the theorem, only in the proof. Otherwise rename
, but not in the statement of the theorem, only in the proof. Otherwise rename 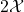 to
to 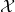 . I sometimes have a hard time noticing factors of two like this, and they get dropped.
. I sometimes have a hard time noticing factors of two like this, and they get dropped.
2. The control of an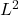 oscillation of a function by the
oscillation of a function by the 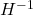 norm of its gradient is proved in our “other” book with Mourrat and Kuusi, see Lemma 1.13. (The proof is to show that the estimate is a consequence of basic energy estimates for a Neumann problem in a cube.)
norm of its gradient is proved in our “other” book with Mourrat and Kuusi, see Lemma 1.13. (The proof is to show that the estimate is a consequence of basic energy estimates for a Neumann problem in a cube.)
By the way, we have been lazy about updating our book, but we have fixed thousands Yu of typos, added material completely rewritten chapter 5. An arxiv update will be coming soon, maybe in a month or so….