Scott Armstrong’s research webpage

I am currently working as a CNRS Directeur de recherche at Sorbonne University in the Laboratoire Jacques-Louis Lions (LJLL). I am on leave from my position as Professor of Mathematics at the Courant Institute of Mathematical Sciences at NYU.

My research lies in mathematical physics, probability theory, and partial differential equations, with a particular emphasis on homogenization theory. This field investigates elliptic and parabolic equations, along with the associated diffusion processes, in highly heterogeneous environments.

My recent focus has been on developing rigorous renormalization group methods, inspired by homogenization techniques, and applying them to problems in mathematical physics. For a high-level overview, see the short review article we wrote with T. Kuusi for Proceedings of the ICM 2026. 

Some of our recent work with T. Kuusi and A. Bou-Rabee has been featured in Quanta magazine. 

My research is supported by an ERC Advanced Grant (from Oct 1, 2025 – Sept 30, 2030). I will be considering postdoctoral candidates with strong backgrounds in probability, analysis, and mathematical physics. (A strong background in all three is not necessary.) Inquiries should be directed to scottnarmstrong+erc@gmail.com. 

I am currently co-organizing the PDE and Probability seminar at LJLL. It meets one Thursday afternoon per month for two one-hour talks. 

 

Books/Monographs
  • S. Armstrong, T. Kuusi. Elliptic Homogenization from Qualitative to Quantitative. announcement | arxiv | github  
  • S. Armstrong, T. Kuusi and J.-C. Mourrat. Quantitative Stochastic Homogenization and Large-Scale Regularity. Grundlehren der mathematischen Wissenschaften vol. 352, Springer-Nature, Cham, 2019. full text
Selected Papers
  • S. Armstrong and T. Kuusi. Renormalization group and elliptic homogenization in high contrast. Invent. Math., in press. arXiv | journal | blog post
  • S. Armstrong, A. Bou-Rabee and T. Kuusi. Superdiffusive central limit theorem for a Brownian particle in a critically-correlated incompressible random drift.  arXiv | Quanta | blog post | youtube
  • S. Armstrong and V. Vicol. Anomalous diffusion by fractal homogenization. Ann. PDE, 11 (2025) art. 2, 145p. arXiv | journal | blog post | youtube
  • S. Armstrong and W. Wu. 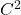C^2 regularity of the surface tension for the 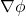\nabla\phi interface model. Comm. Pure Appl. Math., 75 (2022), 349-421. arXiv| journal 
  • S. Armstrong and P. Dario. Elliptic regularity and quantitative homogenization on percolation clusters. Comm. Pure Appl. Math., 71 (2018), 1717-1849. arXiv | journal
  • S. Armstrong, T. Kuusi and J.-C. Mourrat. The additive structure of elliptic homogenization. Invent. Math., 208 (2017), 999-1154. arXiv | journal
  • S. Armstrong and P. Cardaliaguet. Stochastic homogenization of quasilinear Hamilton-Jacobi equations and geometric motions. J. Eur. Math. Soc., 20 (2018), 797-864. arXiv | journal
  • S. N. Armstrong and C. K. Smart. Quantitative stochastic homogenization of convex integral functionals. Ann. Sci. Éc. Norm. Supér., 48 (2016), 423-481. arXiv | journal. 
    This paper received the 2017 SIAG/APDE Prize for most outstanding paper in PDE.
  • Complete list of publications