Power-law superdiffusion in self-similar incompressible random flows

Ahmed Bou-Rabee, Tuomo Kuusi, and I have just uploaded our paper “Superdiffusion and anomalous regularization in self-similar random incompressible flows” to the arXiv. In it we consider the behavior of a diffusion in a multiscale, random divergence-free drift. We prove that the variance of the displacement of the particle grows superlinearly in time with a precise growth exponent, confirming predictions made by physicists in the 1980s.

This superdiffusive behavior can only be caused by a reverse cascade of enhanced diffusivity, propagating across infinitely many scales. Physicists make predictions of this kind using heuristic renormalization group arguments. Our paper can be seen as a fully rigorous implementation of the idea.

Our results were announced in a talk I gave at IHES two weeks ago at a conference celebrating the 75th birthday of Sergiu Klainerman.

Setup and physical motivation

We study the long-time behavior of a Brownian particle advected by a random incompressible drift in $\mathbb{R}^d$ , $d \geq 2$ . The particle position $X_t$ is described by the stochastic differential equation

$\begin{equation*} dX_t = \mathbf{f}(X_t)\,dt + \sqrt{2\nu}\,dW_t\,, \end{equation*}$

where $\nu > 0$ is the molecular diffusivity, $\{W_t\}$ is a standard Brownian motion, and $\mathbf{f}$ is a stationary, isotropic, incompressible random vector field.

Rather than working directly with $\mathbf{f}$ , we parametrize the model in terms of an antisymmetric stream matrix $\mathbf{k}(x)$ , which determines $\mathbf{f}$ by $\mathbf{f} = \nabla \cdot \mathbf{k}$ . We assume $\mathbf{k}$ has a self-similar structure with Hurst exponent $\gamma > 0$ , so that its covariances decay like

$\begin{equation*} \bigl| \mathrm{cov}[\mathbf{f}(x), \mathbf{f}(y)] \bigr| \asymp |x - y|^{-2(1-\gamma)}\,, \quad |x - y| \gg 1\,. \end{equation*}$

Since the drift is incompressible, there are no sources or sinks, and diffusivity is enhanced by the advection. Whether we see genuine superdiffusivity—variance growing faster than linearly in $t$ —depends on the correlation decay exponent $\xi = 2(1 - \gamma)$ . In the 1980s, physicists Bouchaud and Georges predicted the following trichotomy:

$\begin{equation*} \mathbf{E}[|X_t - \mathbf{E}[X_t]|^2] \asymp \begin{cases} t & \text{if } \xi > 2\,, \quad \text{(enhanced diffusivity)} \\ t(\log t)^{\frac12} & \text{if } \xi = 2\,, \quad \text{(borderline superdiffusivity)} \\ t^{4/(2+\xi)} & \text{if } \xi < 2\,. \quad \text{(power-law superdiffusivity)} \end{cases} \end{equation*}$

In the superdiffusive case $\xi < 2$ , the exponent can be rewritten as $\frac{4}{2+\xi} = \frac{2}{2-\gamma}$ . The borderline case $\xi = 2$ (equivalently $\gamma = 0$ ) was the subject of a previous paper of ours; the present paper treats the genuinely superdiffusive regime $\gamma > 0$ .

One of the main physical motivations is Richardson’s $\frac{4}{3}$ law in fluid turbulence, which predicts that the expected squared distance between a pair of particles released at the same location in a turbulent fluid scales like $t^3$ . In this analogy, as explained by the physicists, $X_t$ models the relative displacement of a pair of particles and $\mathbf{f}$ is the difference of fluid velocities felt by the two particles. The parameter $\xi = -\frac{2}{3}$ (equivalently, $\gamma=\frac 43$ ) corresponds to Kolmogorov’s phenomenological theory of turbulence, and plugging into the formula above yields $t^3$ —in exact agreement with Richardson’s $\frac{4}{3}$ law.

Richardson’s original predictions in his 1926 paper were based on empirical data. Kolmogorov’s derivation of it, as well as subsequent derivations, was based essentially on dimensional analysis. Therefore, as noted by Bouchaud and Georges, having a rigorous demonstration (even for a simplified model) is significant.

Heuristic derivation of the exponent

The power-law exponent $\frac{2}{2-\gamma}$ can be derived by tracking the effective diffusivity as a function of scale.

The stream matrix at scale $3^m$ has amplitude $\approx 3^{\gamma m}$ , so the disorder strength grows with scale. The enhancement of diffusivity at each scale is proportional to the square of the disorder, and inversely proportional to the current effective diffusivity $\bar{s}_m$ : when diffusivity is larger, the particle averages over the drift faster, reducing the relative enhancement. This gives a recurrence roughly of the form

$\begin{equation*} \bar{s}_{m+1} \approx \bar{s}_m + \frac{3^{2\gamma m}}{\bar{s}_m}\,. \end{equation*}$

Treating this as a continuous equation in $n = \log_3 R$ , we have $\frac{d(\bar{s}^2)}{dn} \approx\gamma^{-1} 3^{2\gamma n}$ , which integrates to $\bar{s}(R) \approx \gamma^{-\frac12} R^{\gamma}$ .

The time-space relation is $R^2 \approx \bar{s}(R) \cdot t \approx \gamma^{-\frac12} R^{\gamma} \cdot t$ , giving $R \approx \gamma^{-\frac14} t^{1/(2-\gamma)}$ . The variance is therefore

$\begin{equation*} \mathbf{E}[|X_t|^2] \approx R^2 \approx \gamma^{-\frac12} t^{2/(2-\gamma)}\,. \end{equation*}$

Main result: quenched power-law superdiffusivity

Our first main result confirms the physics prediction in the perturbative regime $\gamma \ll 1$ , with precise control of the prefactor.

Theorem A (Quenched power-law superdiffusivity) For $\gamma$ sufficiently small, there exists a constant $c_* > 0$ (the disorder strength, which is explicit in most examples) such that, for a typical realization of the drift, the quenched second moment satisfies

$\begin{equation*} \mathbf{E}^{\mathbf{k},0}[|X_t|^2] = 2d\, c_*^{\frac12} \gamma^{-\frac12}\, t^{\frac{2}{2-\gamma}} \bigl(1 + O(\gamma^{\frac12}|\log \gamma|^3)\bigr)\,, \quad t \gg 1\,. \end{equation*}$

The $O(\gamma^{\frac12}|\log \gamma|^3)$ term is random but has good moment bounds, uniform in the molecular diffusivity $\nu$ .

Several aspects of this result are worth emphasizing:

The result is quenched: it holds for almost every realization of the random drift, not just in expectation over the environment.
We identify the leading prefactor 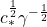$c_*^{\frac12} \gamma^{-\frac12}$ up to a relative error of $O(\gamma^{\frac12}|\log \gamma|^3)$ .
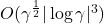The estimates are uniform in the molecular diffusivity $\nu$ .
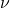There is no homogenization: the errors do not go to zero as the scale becomes large. Rather we see the same thing at every scale (multifractal behavior).

Second main result: anomalous regularization

The renormalization picture has a second, more analytic consequence: anomalous regularization for solutions of the associated elliptic equation.

Theorem C (Anomalous Hölder regularity) For $\gamma$ sufficiently small and $\alpha \leq 1 - C\gamma^{\frac12}$ , solutions of

$\begin{equation*} -\nabla \cdot (\nu I + \mathbf{k}) \nabla u = 0 \end{equation*}$

are Hölder continuous with exponent $\alpha$ , with estimates uniform in $\nu$ .

Even as $\nu \to 0$ , solutions do not lose all regularity. The emergent diffusivity generated by the drift enforces near-Lipschitz behavior on all scales. Since this regularity is uniform in $\nu$ , it cannot be attributed to microscopic smoothing by the $\nu \Delta$ term.

The Hölder exponent $1 - C\gamma^{\frac12}$ is expected to be sharp, reflecting the multifractal nature of the environment.

The proof strategy: Wilsonian renormalization of the generator

Rather than working directly with the trajectories of the SDE, we work with the infinitesimal generator of the process:

$\begin{equation*} L = \nabla \cdot \mathbf{a}(x) \nabla\,, \qquad \mathbf{a}(x) = \nu I + \mathbf{k}(x)\,. \end{equation*}$

The key idea is to coarse-grain this operator scale-by-scale and track a running effective diffusivity $\bar{s}_m$ at each triadic scale $3^m$ . We show that, at every scale,

$\begin{equation*} \bar{s}_m \approx \bigl(\nu^2 + c_* \gamma^{-1} 3^{2\gamma m}\bigr)^{\frac12} \end{equation*}$

up to a relative error of $O(\gamma^{\frac12}|\log \gamma|)$ .

The central object in our analysis is a random “defect” $\mathcal{E}(m)$ which measures how well the heterogeneous operator $L$ is approximated by the constant-coefficient Laplacian $\bar{s}_m \Delta$ on the cube $\square_m$ of side length $3^m$ . We show that $\mathcal{E}(m)$ remains of order $O(\gamma^{\frac12}|\log \gamma|^2)$ at every scale, with good moment bounds uniform in $m$ .

Crucially, the approximation is scale-local: the error does not decay as we go to larger scales, but it remains bounded. This reflects the genuine multifractal nature of the environment. As we zoom out from scale $3^m$ to scale $3^{m+k}$ , we essentially see the same picture again, with the stream matrix resampled at new frequencies.

The central technical challenge is closing the renormalization group induction. At each scale, we must show that the estimates at scale $3^{m+h}$ have the same form as those at scale $3^m$ , with constants that don’t blow up as we iterate. This is far harder than in classical homogenization, where one eventually compares to a fixed homogenized operator.

The difficulty is that there is no fixed microscopic scale to anchor to. Everything must be measured in units of the effective diffusivity $\bar{s}_m$ at the current scale—not in units of $\nu$ . If we measured perturbations in units of $\nu$ , adding a fresh layer $\mathbf{j}_m$ of the stream matrix, which has size $\approx 3^{\gamma m}$ , would produce a catastrophically large error term. But in units of $\bar{s}_m \approx \gamma^{-\frac12} 3^{\gamma m}$ , the perturbation is only $O(\gamma^{\frac12})$ —small enough to be perturbative.

This is what makes the environment a genuine multifractal: fluctuations remain of constant relative size at every scale, and the induction must close purely in these scale-local units.

In most previous works (notably, on the Kraichnan model) proving rigorous results similar to ours, the vector field has a special white-noise-in-time assumption, which allows moment hierarchies to close exactly via Gaussian calculus. This conveniently sidesteps the closure problem entirely by enabling exact computations. Our approach is different, and based on coarse-graining methods originating in quantitative stochastic homogenization, and confronts the closure problem directly.

Setup and physical motivation

Heuristic derivation of the exponent

Main result: quenched power-law superdiffusivity

Second main result: anomalous regularization

The proof strategy: Wilsonian renormalization of the generator

Leave a Comment Cancel Reply